TAMU NanoLab



HOME RESEARCH TEACHING JOBS CONTACT

Nanomagnets

Spin Hall Effect

2-d Metallic State

Mn-12

A microSQUID (about 2 micrometer on a side), made of aluminum.

Mn-6

Earlier Research

NanoSQUIDs - Development and Applications

The first objective of this project is to miniaturize Superconducting Quantum Interference Devices (SQUIDs) to the nanometer regime ("NanoSQUIDs"). SQUIDs are employed as ultra-sensitive magnetic flux detectors in research and industrial applications. Reducing the size of SQUIDs to the micrometer regime ("MicroSQUIDs") has yielded important scientific results in the characterization of magnetic nanoparticles.^1,2 A further reduction in size to the nanometer regime ("NanoSQUIDs") brings this powerful technique to the scale of magnetic single domain particles and individual macromolecules where novel quantum mechanical properties are relevant. NanoSQUIDs are expected to be useful for applications in magnetic characterization, in particular where small spatial resolution or arrays of localized detectors are required.
The second objective is to use NanoSQUIDs for the characterization of molecular nanomagnets. While some initial work in this direction has already yielded interesting results,² a number of important experiments are yet to be implemented. These experiments are driven by new and different molecular nanomagnets as well as the desire to reduce the number of molecular nanomagnets in the system being investigated.
More long-term, the third objective is to implement useful spintronics devices, where NanoSQUIDs and molecular nanomagnets are integrated. The production of NanoSQUIDs is part of a decade-long process of miniaturization of electronic devices, typically referred to as the top-down approach. More recently, largely spurred by important advances in molecular chemistry, the production of appropriate molecular compounds has opened a second alternative towards the goal of creating small, but controlled, systems: the molecular self-assembly into nanoscopic structures, typically referred to as the bottom-up approach. Any useful device created by the bottom-up approach, however, has to be connected to the macroscopic world. Such a connection requires an interface technology between the top-down and the bottom-up approach. In the case of a magnetic system, a NanoSQUID can provide this interface, as it allows for individual access to information in a molecular nanomagnet. Such an integrated system also has the potential of a model quantum computation system³ with integrated readout technique.
This project is expected to develop significant synergy with a recently awarded NSF Nanoscience Interdisciplinary Research Team⁴ at the physics and chemistry departments of Texas A&M University, which is working on the chemical synthesis and physical properties of molecular nanomagnets.

¹ W. Wernsdorfer et al., Phys. Rev. B 55, 11552 (1997). W. Wernsdorfer et al., Phys. Rev. Lett. 78, 1791 (1997). And further work by same group of authors.
² W. Wernsdorfer and R. Sessoli, Science 284, 133 (1999). W. Wernsdorfer et al., Phys. Rev. Lett. 82, 3903 (1999). And further work by same group of authors.
³ J. Tejada et al., cond-mat/0009432, M. Leuenberger et al., cond-mat/0011415.
⁴ Molecular Nanomagnets: Magnetic and Electronic Properties of Novel Magnetic Nanostructures and Nanostructured Materials, D.G. Naugle (PI), G. Agnolet, F.A. Cotton, K.R. Dunbar and V.L. Pokrovsky (duration 2001-2005).

The Spin Hall Effect

The objective of this project is to detect the recently postulated1 Spin Hall Effect (SHE), a physical effect of fundamental importance, which allows the study of pure spin currents and the characterization of spin properties in materials.² It is a topic of considerable pure and applied interest.
To understand the Spin Hall Effect we revert to the Anomalous Hall Effect (AHE).³ In ferromagnetic metals, the Hall resistivity empirically follows ρ_H=R_oB+4R_sM with B being the applied magnetic field, M the magnetization per unit volume and Ro and Rs the ordinary and anomalous Hall coefficient respectively. The first term describes the ordinary Hall effect present in all conductors and resulting from the Lorentz force (Figure 1a). The second term describes the anomalous

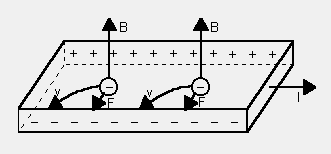
Figure 1: a) Ordinary Hall Effect.

contribution in ferromagnetic materials, which typically exceeds the ordinary Hall effect contribution. The microscopic origin of the AHE is controversial. Explanations like the side jump mechanism and skew scattering by impurities or phonons have been considered.³ Beyond the controversy in origin, the existence of the AHE is experimentally beyond doubt, which provides a sufficient basis for the current discussion. The existence of the AHE indicates that electrons, carrying a spin (and a magnetic moment m), are subject to a transverse force F if they move in a longitudinal current (Figure 1b). Furthermore, electrons with opposing spin directions are subjected to a force in opposing directions. In a ferromagnetic material an applied magnetic field B produces a net magnetization, i.e. more carriers with spin aligned to the applied field than counter aligned. This imbalance of itinerant carrier spins leads to a spin and charge imbalance in the perpendicular direction, which gives rise to the anomalous Hall voltage (Figure 1b).

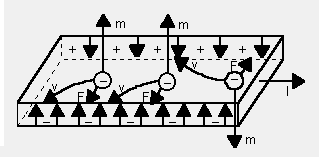
Figure 1: b) AHE contribution in a material with net magnetization. More carriers are deflected to one side, leading to a spin and charge imbalance.

Typically, only the charge imbalance is detected. The spin imbalance is, however, a necessary condition for any spin dependent microscopic description of the AHE.
Next we will focus on the situation which gives rise to the SHE, a material without magnetization and without applied magnetic field. In a material without magnetization, the number of carriers with spin up balances the number of carriers with spin down (Figure 2). Consequently, the same number of carriers is

Figure 2: Spin Hall Effect. In a material without magnetization, the number of carriers with spin up equals the number of carriers with spin down. The same mechanism that leads to the AHE scatters spin up carriers preferentially to one side, while spin down carriers are scattered preferentially to the other side. The resulting spin imbalance leads to a spin potential VSH between opposing sides of the strip.

scattered to one side of a current carrying strip than to the other and no charge imbalance between the different sides of the strip exists. There is, however, an imbalance of spins between the different sides of the strip, since spin up carriers are preferentially scattered to one side, while spin down carriers are preferentially scattered to the other. The resulting spin imbalance gives rise to a spin potential VSH, while the electronic potential is constant as one moves from one side of the strip to the opposite side (Figure 2). VSH is a direct consequence of same microscopic models, leading to the AHE.
To detect the SHE, Hirsch suggested an elegant analogy to a double Hall effect device. The idea is that a perpendicular cross strip connects the opposite sides of the current carrying strip. In case of double Hall effect at B>0 (Figure 3a), the electronic

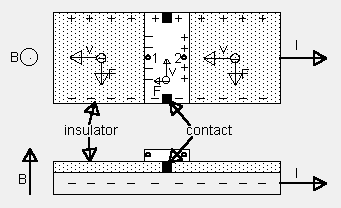
Figure 3: a) Same device in B=0. The SHE leads to an electronic potential between point 1 and 2, though no Lorentz forces are acting on carriers.

potential in the current carrying strip induces a perpendicular current in the cross strip, which itself is subject to the Lorentz force. Consequently, an electronic potential between point 1 and point 2 in Fig. 3 a exists. In case of the SHE (at B=0), the spin imbalance produced in the current carrying strip migrates into the opposite ends of the cross strip (Figure 3b). Inside the

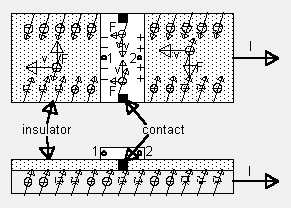
Figure 3: b) Double Hall Effect in a tri-layer structure. The top cross strip is insulated from the current carrying strip underneath except for two contact points. Lorentz forces lead to a potential between point 1 and 2.

cross strip there is, however, no reason why a spin imbalance should remain. Consequently, a spin current flows in the cross strip which itself is subject to the spin scattering mechanism. As can be seen in the cross strip of Figure 3b, electrons of opposing spin direction are flowing towards each other to eliminate the spin imbalance. Due to the same force that lead to the spin separation in the current carrying strip, they are scattered towards the same side of the cross strip. The result is an electronic potential between point 1 and point 2, which can be measured as a voltage. Hirsch calculates the size of the expected voltage in Aluminum to be 58nV, based on lithographic length scales, idealized interfaces, perfect alignment and work by Johnson and Silsbee.⁴
Discovering the postulated SHE and investigating its details will have several benefits for fundamental and applied physics. Fundamentally, this experiment would produce a pure spin current and would investigate the interrelations of spin and charge currents. Furthermore it would show that a skew scattering mechanism exists even in a paramagnetic material and is thus a more general phenomenon. This would aid in the understanding of the AHE, one of the more significant outstanding issues in condensed matter physics. On the applied side, this project would provide information on the spin diffusion length and its dependence on material properties. The understanding of the material dependence of spin diffusion length and spin-related scattering will aid technologists in the selection of materials for spin electronics devices.

¹ J. E. Hirsch, Phys. Rev. Lett. 83, 1834 (1999).
² S. Zhang, Phys. Rev. Lett. 85, 393 (2000).
³ C. M. Hurd, The Hall Effect in Metals and Alloys",
   Plenum, New York, 1973, Chapter 5.
⁴ M. Johnson and R. H. Silsbee,
   Phys. Rev. Lett. 55, 1790 (1985);
   Phys. Rev. B 37, 5312 (1988).

A Metal-Insulator transition in 2-dimensional Gd_xSi_1-x?

This project has the following objectives:

1. To help answer the fundamental question: Is there a metallic state and thus a Metal-Insulator transition in 2 dimensions? And if so,

2. To measure the density of states in an in-situ tunable material in 2 dimensions and determine the critical exponent.

The existence of a Metal-Insulator transition in 2 dimensions is a disputed topic. While the existence of a metallic state in 3 dimensions is beyond doubt there is strong evidence that the existence of any amount of disorder will lead to an insulating state in 1 dimension. The 2-dimensional case is of particular interest since it is believed to be a borderline case. While it has been thought for some time, that a metallic state cannot exist in 2 dimensions, subsequent work has put this conclusion in doubt.² Furthermore, there have been several experimental results that suggest the existence of a metallic state in 2 dimensions.² Here I propose an experiment, which measures the density of states of a 2-dimensional material, whose disorder can be reversibly tuned in-situ. Working as a post-doc with Bob Dynes at the University of California, San Diego and in collaboration with Frances Hellman (UCSD), we have recently conducted the equivalent experiment in 3 dimensions.³ We found, that the results in the limiting metallic and insulating cases are well described by existing theories and that the density of states in the transition region could be determined to unprecedented quantitative precision (see Figure).

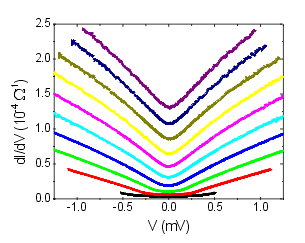
Figure: The density of states of Gd_xSi_1-x at the
Metal-Insulator Transition.

As a result, the critical exponent of the density of states in the critical regime of the 3-dimensional metal insulator transition could for the first time be determined (it is 2).⁴ This project is an ongoing collaboration with Bob Dynes, Frances Hellman and co-workers.

¹P. A. Lee and T. V. Ramakrishnan,
   Rev. Mod. Phys. 57, 287 (1985).
²E. Abrahams, S. V. Kravchenko and M. P. Sarachik,
   Rev. Mod. Phys. 73, 251 (2001).
³W. Teizer, F. Hellman and R. C. Dynes,
   Phys. Rev. Lett. 85, 848 (2000).
⁴W. Teizer, F. Hellman and R. C. Dynes,
   to be published.